Im ersten Artikel dieser Reihe hatte ich eine VBA Funktion vorgestellt, um große Zahlen in Excel addieren zu können. Prinzip hierbei ist, die in Strings abgelegten Zahlen blockweise zu addieren und anschließend die Blöcke wieder zusammenzufügen.
Dieser Artikel stellt nun eine VBA Funktion vor, um eine Subtraktion großer Zahlen durchzuführen; auch hier werden wir die Zahlen in Blöcke aufteilen, jedoch aber zusätzlich einen kleinen Trick anwenden.
Subtraktion von großen Zahlen in Excel
Im folgenden Bild sind die zwei Ausgangszahlen X und Y zu sehen. Die hier vorgestellte Funktion wird allerdings nur dann korrekt ablaufen, wenn beide Zahlen positiv sind und zudem X größer Y ist. Für spätere Berechnungen ist dies ausreichend, denn eine Subtraktion der Form „X – Y mit X < Y“ lässt sich durch eine Vorzeichenumkehr in das gewünschte Format umwandeln: „-(Y - X) mit Y > X“.
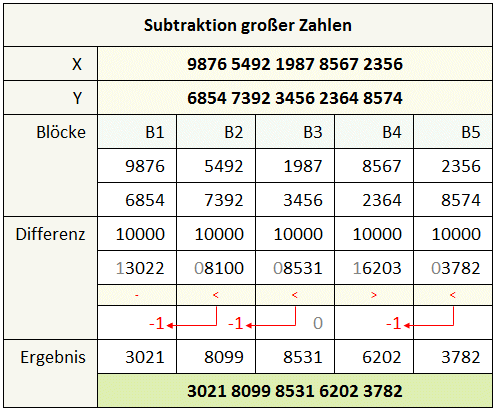
Wie im vorherigen Artikel detaillierter erläutert, werden auch hier die Eingangsparameter in Blöcke aufgeteilt. Im oberen Beispielbild sind insgesamt 5 Blöcke à je vier Ziffern abgebildet. Eine Subtraktion kann, rechentechnisch gesehen, auf eine Addition des Minuenden (im Beispiel die Zahl X) und dem Neunerkomplement des Subtrahenden (im Beispiel die Zahl Y) zurückgeführt werden. Das Neunerkomplement wird durch die Differenz jeder Ziffer zur Zahl 9 gebildet. Aufbauend auf dieser Logik kann die Subtraktion als „Nächste Zehnerpotenz + Minuend – Subtrahend – Übertrag = Ergebnis mit oder ohne Übertrag für Nachfolger“ formuliert werden.
So ist die nächste Zehnerpotenz einer vierstelligen Zahl genau 10000, wenn wir das Beispiel zum Block B5 betrachten, erhalten wir dann „10000 – 8574 + 2356 = 3782 und ein Ergebnis kleiner 10000. Dies heißt, dass im nächsten Block der Übertrag 1 abzuziehen ist. In derselben Art kann für die weiteren Blöcke von rechts nach links vorgegangen werden. Schauen wir uns dieses wieder im Code an:
Wie im Code zur Addition zweier großer Zahlen, werden in einem ersten Schritt die Eingangsparameter „x“ und „y“ auf die Länge geprüft und anschließend in der Variable „lngLength“ die Länge des Parameters festgehalten, der die größte Anzahl an Ziffern beinhaltet.
Die Variable „lngPrecision“ wird anschließend so berechnet, dass eine optimale Blocklänge entsteht. Zudem werden die Eingangsparameter in der Art umgeformt, dass sie die gleiche Länge aufweisen und diese Länge wiederrum durch die Blocklänge ganzzahlig teilbar ist.
Die Variable „dblCalc_Delta“ wird mit der nächstgrößeren Zehnerpotenz gefüllt, wobei sich diese aus der Blocklänge nach dem Schema „1 und N angehängte Nullen, N = Blocklänge“ berechnet. Es folgt eine Schleife, die nun die Berechnung zur Differenz pro Block ausführt. Nach jedem Zwischenwert wird ermittelt, ob ein Übertrag notwendig ist oder nicht. Und das Teilergebnis wird an dem Gesamtergebnis vorangestellt, wobei auch zu beachten ist, dass keine Nullen verloren gehen.
Schließlich werden alle eventuell überschüssig entstandenen Führungsnullen vom Gesamtergebnis entfernt. Somit wäre die Funktion zur Subtraktion fertig. Im nächsten Artikel werde ich dann die Multiplikation von zwei großen Zahlen implementieren und hierbei den Algorithmus von Karatsuba verwenden.

